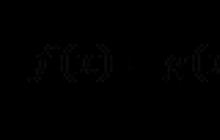Odz kvadratna enačba. Razpon sprejemljivih vrednosti: teorija in praksa. Reševanje kvadratne enačbe s tangento

Znanstveni svetnik:

1. Uvod 3

2. Zgodovinska skica 4

3. “Mesto” ODZ pri reševanju enačb in neenačb 5-6

4. Lastnosti in nevarnosti ODZ 7

5. ODZ – obstaja rešitev 8-9

6. Iskanje ODZ je dodatno delo.

Ekvivalentnost prehodov 10-13

7. ODZ na Enotnem državnem izpitu 14-15

8. Sklep 16

9. Literatura 17

1. Uvod

Enačbe in neenačbe, v katerih je treba najti območje sprejemljivih vrednosti, niso našle mesta v algebrskem tečaju sistematičnega podajanja, zato se morda moji vrstniki pogosto zmotijo ​​pri reševanju takšnih primerov in porabijo veliko časa za reševanje jih, pri tem pa pozabimo na razpon sprejemljivih vrednosti. To je določilo problem tega dela.

V tem delu je namenjeno raziskovanju pojava obstoja območja sprejemljivih vrednosti pri reševanju enačb in neenakosti različnih vrst; analizirajte to situacijo, pripravite logično pravilne zaključke v primerih, kjer morate upoštevati obseg sprejemljivih vrednosti.

Naloge:

Na podlagi obstoječih izkušenj in teoretičnih osnov zbrati osnovne informacije o razponu dovoljenih vrednosti in njegovi uporabi v šolski praksi; Analizirati rešitve različnih vrst enačb in neenačb (ulomkov-racionalnih, iracionalnih, logaritemskih, ki vsebujejo inverzne trigonometrične funkcije); Preverite predhodno pridobljene rezultate pri reševanju različnih enačb in neenačb, se prepričajte o zanesljivosti metod in metod za njihovo reševanje; Določite "mesto" območja sprejemljivih vrednosti pri reševanju enačb in neenakosti; Uporabite raziskovalne materiale, pridobljene v situaciji, ki se razlikuje od standardne, in jih uporabite pri pripravi na enotni državni izpit.

Pri reševanju teh problemov so bili uporabljeni naslednji raziskovalne metode: analiza, statistična analiza, dedukcija, klasifikacija, napovedovanje.

Študija se je začela s ponavljanjem dobro znanih funkcij, ki so jih preučevali v šolskem kurikulumu. Obseg mnogih od njih je omejen.

Razpon sprejemljivih vrednosti se pojavi pri reševanju: delnih racionalnih enačb in neenačb; iracionalne enačbe in neenačbe; logaritemske enačbe in neenačbe; enačbe in neenačbe, ki vsebujejo inverzne trigonometrične funkcije.

Po reševanju številnih primerov iz različnih virov (učbeniki USE, učbeniki, referenčne knjige) smo ugotovili rešitev primerov po naslednjih načelih:

· lahko rešite primer in upoštevate ODZ (najpogostejša metoda)

· primer je mogoče rešiti brez upoštevanja ODZ

· le z upoštevanjem ODZ je mogoče priti do prave odločitve.

Preučena je bila analiza rezultatov enotnega državnega izpita v preteklih letih. Veliko napak je bilo storjenih pri primerih, v katerih je treba upoštevati DL. Praktični pomen Delo je v tem, da se lahko njegova vsebina, ocene in zaključki uporabljajo pri poučevanju matematike v šoli, pri pripravi na zaključno spričevalo šolarjev v 9. in 11. razredu.

2. Zgodovinska skica

Tako kot drugi pojmi matematike se tudi koncept funkcije ni razvil takoj, ampak je šel skozi dolgo pot razvoja. V delu P. Fermata "Uvod in študij ravnih in trdnih mest" (1636, objavljeno 1679) je rečeno: "Kadar koli sta v končni enačbi dve neznani količini, obstaja mesto." V bistvu govorimo o funkcionalni odvisnosti in njenem grafičnem prikazu (»mesto« pri Fermatu pomeni črta). Preučevanje črt glede na njihove enačbe v "Geometriji" R. Descartesa (1637) prav tako kaže na jasno razumevanje medsebojne odvisnosti dveh spremenljivk. I. Barrow (Lectures on Geometry, 1670) v geometrijski obliki ugotavlja medsebojno inverzno naravo dejanj diferenciacije in integracije (seveda brez uporabe samih izrazov). Že to kaže na povsem jasno obvladovanje pojma funkcije. Ta koncept v geometrijski in mehanski obliki najdemo tudi pri I. Newtonu. Vendar pa se izraz "funkcija" prvič pojavi šele leta 1692 pri G. Leibnizu in poleg tega ne povsem v njegovem sodobnem razumevanju. G. Leibniz imenuje različne segmente, povezane s krivuljo (na primer absciso njenih točk), funkcijo. V prvem natisnjenem tečaju, "Analiza infinitezimalij za poznavanje ukrivljenih črt" L'Hopitala (1696), izraz "funkcija" ni uporabljen.

Prvo definicijo funkcije v smislu, ki je blizu sodobnemu, najdemo v I. Bernoulliju (1718): "Funkcija je količina, sestavljena iz spremenljivke in konstante." Ta ne povsem jasna definicija temelji na ideji določanja funkcije z analitično formulo. Ista ideja se pojavlja v definiciji L. Eulerja, ki jo je podal v "Uvodu v analizo neskončnega" (1748): "Funkcija spremenljive količine je analitični izraz, sestavljen na nek način iz te spremenljive količine in števil oz. stalne količine." L. Eulerju pa ni več tuje sodobno razumevanje funkcije, ki pojma funkcije ne povezuje z nobenim od njenih analitičnih izrazov. Njegov »Diferencialni račun« (1755) pravi: »Kadar so nekatere količine odvisne od drugih na tak način, da so ob spreminjanju slednjih tudi same podvržene spremembam, potem se prve imenujejo funkcije drugih.«

Od začetka 19. stoletja se pojem funkcije vedno bolj opredeljuje brez omembe njene analitične reprezentacije. V "Razpravi o diferencialnem in integralskem računu" (1797-1802) S. Lacroix pravi: "Vsaka količina, katere vrednost je odvisna od ene ali več drugih količin, se imenuje funkcija teh slednjih." V »Analitični teoriji toplote« J. Fourierja (1822) je stavek: »Funkcija f(x) označuje popolnoma poljubno funkcijo, to je zaporedje danih vrednosti, ne glede na to, ali je predmet splošnega zakona ali ne in ustreza vsem vrednostim x vsebuje med 0 in neko vrednostjo x" Definicija N. I. Lobačevskega je blizu sodobni: "... Splošni koncept funkcije zahteva, da funkcija iz x poimenujte številko, ki je podana za vsako x in skupaj z x postopoma spreminja. Vrednost funkcije je lahko podana bodisi z analitičnim izrazom bodisi s pogojem, ki omogoča testiranje vseh števil in izbiro enega od njih, ali pa lahko odvisnost obstaja in ostane neznana. Tam je tudi rečeno malo nižje: "Širok pogled na teorijo dopušča obstoj odvisnosti samo v smislu, da so števila ena z drugim v povezavi razumljena, kot da so dana skupaj." Tako je bila sodobna definicija funkcije, brez sklicevanja na analitično nalogo, običajno pripisana P. Dirichletu (1837), pred njim večkrat predlagana:

y ima funkcijo spremenljivke x (na segmentu https://pandia.ru/text/78/093/images/image002_83.gif" width="95" height="27 src=">. S kvadriranjem obeh stranic enačbe, se znebimo iracionalnosti. Toda bodimo pozorni na dejstvo, da kvadriranje na splošno ni ekvivalentna transformacija in pri kvadriranju lahko dobimo dodatne korene. Če so koreni celi, potem je enostavno Toda v nekaterih primerih je preverjanje neprijetno. Nato uporabite redukcijo te enačbe na enakovredni sistem:

.

V tem primeru ni treba najti ODZ: iz prve enačbe sledi, da dobljene vrednosti x izpolnjujejo naslednjo neenakost: https://pandia.ru/text/78/093/images/image005_34. gif" width="107" height="27 src="> je sistem:

Ker v enačbo vstopijo enako, lahko namesto neenakosti vključite neenakost https://pandia.ru/text/78/093/images/image010_15.gif" width="220" height="49">

https://pandia.ru/text/78/093/images/image015_10.gif" width="239" height="51">

3. Reševanje logaritemskih enačb in neenačb.

3.1. Shema za reševanje logaritemske enačbe

Dovolj pa je, da preverite samo en pogoj ODZ.

3.2..gif" width="115" height="48 src=">.gif" width="115" height="48 src=">

4. Trigonometrične enačbe oblike so enakovredni sistemu (namesto neenakosti lahko v sistem vključite neenakost https://pandia.ru/text/78/093/images/image025_2.gif" width="377" height="23"> so enakovredni k enačbi

4. Značilnosti in nevarnosti območja dovoljenih vrednosti

Pri pouku matematike moramo v vsakem primeru najti DL. Hkrati glede na matematično bistvo zadeve iskanje ODZ sploh ni obvezno, pogosto ni potrebno, včasih pa tudi nemogoče - in vse to brez škode za rešitev primera. Po drugi strani pa se pogosto zgodi, da šolarji po reševanju primera pozabijo upoštevati DL, ga zapišejo kot končni odgovor in upoštevajo le nekatere pogoje. Ta okoliščina je dobro znana, vendar se "vojna" nadaljuje vsako leto in bo, kot kaže, trajala še dolgo.

Upoštevajte na primer naslednjo neenakost:

Tu se išče ODZ in reši neenačba. Šolarji pa pri reševanju te neenačbe včasih menijo, da je povsem mogoče brez iskanja ODZ, natančneje brez pogoja

Pravzaprav je za pravilen odgovor potrebno upoštevati neenakost , in .

Ampak, na primer, rešitev enačbe: https://pandia.ru/text/78/093/images/image033_3.gif" width="79 height=75" height="75">

kar je enakovredno delu z ODZ. Vendar je v tem primeru takšno delo nepotrebno - dovolj je preveriti izpolnjevanje samo dveh od teh neenakosti in poljubnih dveh.

Spomnimo se, da je vsako enačbo (neenakost) mogoče zmanjšati na obliko . ODZ je preprosto domena definicije funkcije na levi strani. Da je to področje potrebno spremljati, izhaja iz definicije korena kot števila iz domene definicije dane funkcije, torej iz ODZ. Tukaj je smešen primer na to temo..gif" width="20" height="21 src="> ima domeno definicije nabora pozitivnih števil (to je seveda dogovor, da upoštevamo funkcijo z , vendar razumno), in potem -1 ni koren.

5. Razpon sprejemljivih vrednosti - obstaja rešitev

In končno, v številnih primerih vam iskanje ODZ omogoča, da dobite odgovor brez okornih izračunov ali celo ustno.

1. OD3 je prazna množica, kar pomeni, da izvirni primer nima rešitev.

1) 2) 3)

2. B ODZ najdemo eno ali več števil in preprosta zamenjava hitro določi korenine.

1) , x=3

2)Tukaj v ODZ je samo številka 1 , in po zamenjavi je jasno, da ni koren.

3) V ODZ sta dve številki: 2 in 3 in oba sta primerna.

4) > V ODZ sta dve številki 0 in 1 , in ustreza samo 1 .

ODZ se lahko učinkovito uporablja v kombinaciji z analizo samega izraza.

5) < ОДЗ: Но в правой части неравенства могут быть только положительные числа, поэтому оставляем x=2. Nato nadomestimo v neenakost 2 .

6) Iz ODZ sledi, kjer imamo ..gif" width="143" height="24"> Iz ODZ imamo: . Potem pa in . Ker ni rešitev.

Iz ODZ imamo:..gif" width="53" height="24 src=">.gif" width="156" height="24"> ODZ: . Od takrat

Na drugi strani,. Enakost je mogoča le, če sta obe strani enačbe enaki 0 , torej kdaj x=1. Po zamenjavi te vrednosti X Prepričani smo, da rešitev ni.

ODZ:. Razmislite o enačbi na intervalu [-1; 0).

Izpolnjuje naslednje neenakosti https://pandia.ru/text/78/093/images/image072_0.gif" width="68" height="24 src=">.gif" width="123" height="24 src="> in ni rešitev. S funkcijo in https://pandia.ru/text/78/093/images/image077_0.gif" width="179" height="25">. ODZ: x>2. pri čemer . To pomeni, da je začetna enakost nemogoča in da ni rešitev.

Zdaj pa navedimo primer, ki ga je predlagal učitelj pri lekciji algebre. Tega nismo mogli rešiti takoj, ko pa smo našli ODZ, je postalo vse jasno.

Poiščite koren celega števila enačbe https://pandia.ru/text/78/093/images/image080_0.gif" width="124" height="77">

Celoštevilska rešitev je možna le, če x=3 in x=5. S preverjanjem ugotovimo, da je koren x=3 ne ustreza, zato je odgovor: x=5.

6. Iskanje obsega sprejemljivih vrednosti je dodatno delo. Ekvivalentnost prehodov.

Lahko navedete primere, kjer je situacija jasna tudi brez iskanja DZ.

1.

Enakost je nemogoča, ker mora biti pri odštevanju večjega izraza od manjšega rezultat negativno število.

2. .

Vsota dveh nenegativnih funkcij ne more biti negativna.

Navedel bom tudi primere, ko je iskanje ODZ težko, včasih pa preprosto nemogoče.

In končno, iskanje ODZ je zelo pogosto le dodatno delo, brez katerega lahko storite, s čimer dokažete svoje razumevanje dogajanja. Tukaj lahko navedemo ogromno primerov, zato bomo izbrali le najbolj značilne. Glavna metoda reševanja v tem primeru so ekvivalentne transformacije pri prehodu iz ene enačbe (neenakosti, sistema) v drugo.

1.. ODZ ni potreben, ker, po ugotovitvi teh vrednosti X, pri katerem x2=1, ne moremo dobiti x=0.

2. . ODZ ni potreben, saj ugotovimo, kdaj je radikalni izraz enak pozitivnemu številu.

3. . ODZ ni potreben iz istih razlogov kot v prejšnjem primeru.

4.

ODZ ni potreben, ker je radikalni izraz enak kvadratu neke funkcije in zato ne more biti negativen.

5.

6. . ODZ ni potreben, saj je izraz vedno pozitiven.

7. Za rešitev je dovolj samo ena omejitev za radikalni izraz. Pravzaprav iz zapisanega mešanega sistema sledi, da je drugi radikalni izraz nenegativen.

8. DZ ni potreben iz istih razlogov kot v prejšnjem primeru.

9. ODZ ni potreben, saj je dovolj, da sta dva od treh izrazov pod logaritemskimi predznaki pozitivna, da zagotovimo pozitivnost tretjega.

10. .gif" width="357" height="51"> ODZ ni potreben iz istih razlogov kot v prejšnjem primeru.

Omeniti pa velja, da pri reševanju z metodo ekvivalentnih transformacij pomaga poznavanje ODZ (in lastnosti funkcij).

Tukaj je nekaj primerov.

1. . OD3, kar pomeni, da je izraz na desni strani pozitiven in je v tej obliki mogoče zapisati enačbo, ki je enakovredna tej. Dobljeni rezultat je treba preveriti z ODZ.

2. ODZ: . Toda takrat in pri reševanju te neenakosti ni treba upoštevati primera, ko je desna stran manjša od 0.

3. . Iz ODZ izhaja, da je torej izključen primer, ko je .

Na splošno se zdi, da je učinkovitost metode ekvivalentnih transformacij jasna. Z njihovo pomočjo pridemo do odgovora brez iskanja DZ. Ali to pomeni, da obstaja neka univerzalna metoda in je treba le še naučiti se jo uporabljati? Vendar ni tako. Razlogov za to je več. Izrekov o ekvivalentnih transformacijah je precej, ni si jih lahko zapomniti in samozavestno obvladati jih ni lahko. Pogosto z uporabo enakovrednih transformacij začnete postavljati ta znak na kakršne koli prehode iz ene enačbe v drugo, tako resnično enakovredne kot ne tako. Ti izreki so hitro pozabljeni.

Težava je tudi v tem, da lahko pri pisanju enakovrednosti pozabite zapisati vse pogoje, ki jo zagotavljajo, vendar to ne sme na noben način vplivati ​​na odgovor. Tukaj sta dva taka primera:

1. Prehod na splošno izgleda takole:

V tem primeru je izraz pod znakom logaritma na desni vedno pozitiven. Zato v zvezi s tem primerom tisti del ekvivalenčnih pogojev, ki je zapisan kot niz, ne doda ničesar. Toda, ko ste sprejeli takšno odločitev, lahko preprosto pozabite na to celoto.

Obstajata dva možna primera: 0<<1 и >1.

To pomeni, da je prvotna neenakost enakovredna naslednjemu nizu sistemov neenakosti:

Prvi sistem nima rešitev, iz drugega pa dobimo: x<-1 – решение неравенства.

Razumevanje pogojev enakovrednosti zahteva poznavanje nekaterih tankosti. Na primer, zakaj so naslednje enačbe enakovredne:

oz

In končno, morda najpomembnejše. Dejstvo je, da enakovrednost zagotavlja pravilnost odgovora, če se izvede nekaj transformacij same enačbe, ne pa se uporablja za transformacije le v enem od delov. Ekvivalenčni izreki ne zajemajo okrajšav in uporabe različnih formul v enem od delov. Nekaj ​​primerov te vrste je bilo navedenih v delu. Poglejmo še nekaj primerov.

1. Ta odločitev je naravna. Na levi strani glede na lastnost logaritemske funkcije preidemo na izraz. Kot rezultat dobimo enačbo. Je enakovreden takemu sistemu

Po rešitvi tega sistema dobimo rezultat (-2 in 2), ki pa ni odgovor, saj števila -2 ni vključeno v ODZ. Torej, ali moramo namestiti ODS? Seveda ne. Ker pa smo v rešitvi uporabili določeno lastnost logaritemske funkcije, smo dolžni podati pogoje, pod katerimi je ta izpolnjena. Tak pogoj je pozitivnost izrazov pod znakom logaritma..gif" width="65" height="48">.

2. ..gif" width="143" height="27">.gif" width="147" height="24">dodajte pogoj in takoj boste videli, da je samo številka https://pandia.ru/ izpolnjuje ta pogoj text/78/093/images/image129.gif" width="117" height="27">) je dokazalo 52 % tistih, ki so opravljali test. Eden od razlogov za tako nizke stopnje je dejstvo, mnogi diplomanti niso izbrali korenov, dobljenih iz enačbe po kvadriranju.

3) Razmislite na primer o rešitvi ene od težav C1: »Poiščite vse vrednosti x, za katere so točke grafa funkcije ležijo nad ustreznimi točkami na grafu funkcije. Naloga se skrči na reševanje ulomkov neenačbe, ki vsebuje logaritemski izraz. Poznamo metode za reševanje takih neenakosti. Najpogostejša med njimi je intervalna metoda. Pri njegovi uporabi pa testiranci delajo različne napake. Oglejmo si najpogostejše napake na primeru neenakosti:

1. Diplomanti pravilno najdejo DL z reševanjem sistema neenačb:

kje x . Nato z množenjem obeh strani neenakosti s skupnim imenovalcem dobimo neenakost: log(23 - 10 x

2..gif" width="124" height="29">. Naslednji dobijo x– 10 +; . Z rešitvijo te enačbe in ob upoštevanju pogoja diplomanti sklepajo, da enačba nima rešitev.

3. Testiranci pravilno pretvorijo enačbo v obliko

in razmislite o dveh primerih: x 10 in x < 10. Они отмечают, что в первом случае решений нет, а во втором – корнями являются числа –1 и . При этом выпускники не учитывают условие x < 10.

8. Zaključek

V tem delu smo poskušali raziskati pojav obstoja razpona sprejemljivih vrednosti pri reševanju enačb in neenačb različnih vrst, analizirali to situacijo in naredili logično pravilne zaključke v primerih, kjer je treba upoštevati razpon sprejemljivih vrednosti. Zame se je tema "Območje dovoljenih vrednosti" zdela zelo zapletena in nerazumljiva, v šolskih učbenikih pa ta tema nima ustreznega mesta, praktično ni zajeta, čeprav naloge enotnega državnega izpita vsebujejo naloge za reševanje enačb in neenakosti, v katerih treba je najti območje dovoljenih vrednosti . V procesu dela smo se soočili z dejstvom, da literature na to temo ni dovolj za celovito in sistematično študijo. Menimo, da ta tema zahteva veliko pozornosti matematikov in metodologov.

Po rešitvi številnih primerov iz različnih virov lahko potegnemo nekaj zaključkov: ni univerzalne metode za reševanje enačb in neenačb. Vsakič, če želite razumeti, kaj počnete, in ne delovati mehanično, pomislite: katero metodo rešitve bi morali izbrati, zlasti ali bi morali iskati območje sprejemljivih vrednosti ali ne? Verjamemo, da bodo pridobljene izkušnje pomagale rešiti to dilemo. Učenci bodo prenehali delati napake, če se bodo naučili pravilno uporabljati obseg sprejemljivih vrednosti. Ali nam bo to uspelo, bo pokazal čas, oziroma prihajajoči enotni državni izpit 2010.

Upamo, da bo predstavljeno delo učiteljem in učencem zanimivo in uporabno ter da učne motnje ne bodo več "nekakšen slab ODZ" za šolarje.

9. Literatura

1. itd. “Algebra in začetki analize 10-11” knjiga in učbenik, M.: “Prosveshchenie”, 2002.

2. “Priročnik za osnovno matematiko.” M.: "Znanost", 1966.

3. Časopis "Matematika" št. 46,

4. Časopis "Matematika" št.

5. Časopis "Matematika" št.

6. "Zgodovina matematike v šoli, razredi VII-VIII." M.: "Razsvetljenje", 1982.

7. itd. »Najpopolnejša izdaja možnosti za naloge resničnega enotnega državnega izpita: 2009/FIPI« - M.: »Astrel«, 2009.

8. in drugi »Enotni državni izpit. Matematika. Univerzalni materiali za pripravo študentov / FIPI" - M.: "Intelekt Center", 2009.

9. in drugi “Algebra in začetki analize 10-11.” M.: "Razsvetljenje", 2007.

10. , “Delavnica reševanja nalog pri šolski matematiki (delavnica algebra).” M.: Izobraževanje, 1976.

11. "25.000 lekcij matematike." M.: "Razsvetljenje", 1993.

12. "Pripravljamo se na matematične olimpijade." M.: "Izpit", 2006.

13. “Enciklopedija za otroke “MATEMATIKA”” zvezek 11, M.: Avanta +; 2002.

14. Gradiva s strani http://www. *****, http://www. *****.

Internetni portal Wikipedia http://ru. wikipedia. org/wiki/Numeric_function (dostopano 3. 5. 2010).

, “Delavnica reševanja nalog pri šolski matematiki (delavnica algebra).” M.: Izobraževanje, 1976, str.64.

Vprašanje študenta na Odgovore@***** http://otvet. *****/question/8166619/ (Datum ogleda 22.03.2010)

Metodološko pismo "O uporabi rezultatov enotnega državnega izpita 2008 pri poučevanju matematike v izobraževalnih ustanovah srednjega (popolnega) splošnega izobraževanja" http://www. ***** (Datum ogleda 17.12.2009)

Ohranjanje vaše zasebnosti je za nas pomembno. Iz tega razloga smo razvili Politiko zasebnosti, ki opisuje, kako uporabljamo in shranjujemo vaše podatke. Preglejte naše postopke varovanja zasebnosti in nam sporočite, če imate kakršna koli vprašanja.

Zbiranje in uporaba osebnih podatkov

Osebni podatki se nanašajo na podatke, ki jih je mogoče uporabiti za identifikacijo ali vzpostavitev stika z določeno osebo.

Kadar koli stopite v stik z nami, boste morda morali posredovati svoje osebne podatke.

Spodaj je nekaj primerov vrst osebnih podatkov, ki jih lahko zbiramo, in kako lahko te podatke uporabimo.

Katere osebne podatke zbiramo:

• Ko na spletnem mestu oddate prijavo, lahko zberemo različne podatke, vključno z vašim imenom, telefonsko številko, e-poštnim naslovom itd.

Kako uporabljamo vaše osebne podatke:

• Osebni podatki, ki jih zbiramo, nam omogočajo, da vas kontaktiramo z edinstvenimi ponudbami, promocijami in drugimi dogodki ter prihajajočimi dogodki.
• Občasno lahko uporabimo vaše osebne podatke za pošiljanje pomembnih obvestil in sporočil.
• Osebne podatke lahko uporabljamo tudi za interne namene, kot so izvajanje revizij, analize podatkov in različne raziskave, da bi izboljšali storitve, ki jih nudimo, in vam dali priporočila glede naših storitev.
• Če sodelujete v nagradni igri, tekmovanju ali podobni promociji, lahko podatke, ki nam jih posredujete, uporabimo za upravljanje takih programov.

Razkritje informacij tretjim osebam

Prejetih podatkov ne razkrivamo tretjim osebam.

Izjeme:

• Če je potrebno - v skladu z zakonom, sodnim postopkom, v sodnem postopku in/ali na podlagi javnih zahtev ali zahtev državnih organov na ozemlju Ruske federacije - za razkritje vaših osebnih podatkov. Podatke o vas lahko razkrijemo tudi, če ugotovimo, da je takšno razkritje potrebno ali primerno za varnostne namene, namene kazenskega pregona ali druge javno pomembne namene.
• V primeru reorganizacije, združitve ali prodaje lahko osebne podatke, ki jih zberemo, prenesemo na ustrezno naslednico tretje osebe.

Varstvo osebnih podatkov

Izvajamo previdnostne ukrepe – vključno z administrativnimi, tehničnimi in fizičnimi – za zaščito vaših osebnih podatkov pred izgubo, krajo in zlorabo ter nepooblaščenim dostopom, razkritjem, spreminjanjem in uničenjem.

Spoštovanje vaše zasebnosti na ravni podjetja

Da bi zagotovili varnost vaših osebnih podatkov, svojim zaposlenim sporočamo standarde zasebnosti in varnosti ter strogo uveljavljamo prakse glede zasebnosti.

Čestitke, dragi bralci!

Končno smo prispeli reševanje trigonometričnih enačb. Zdaj bomo rešili več enačb, ki so podobne nalogam enotnega državnega izpita. Seveda bodo na pravem izpitu naloge nekoliko težje, a bistvo bo ostalo enako.

Najprej si poglejmo enostavno enačbo (podobne smo že reševali v prejšnjih lekcijah, vendar je ponavljanje vedno koristno).

$$(2\cos x + 1) (2\sin x - \sqrt(3)) = 0.$$

Mislim, da so razlage, kako se odločiti, nepotrebne.

$$2\cos x + 1 = 0 \text( ali ) 2\sin x - \sqrt(3) =0,$$

$$\cos x = -\frac(1)(2) \text( ali ) \sin x = \frac(\sqrt(3))(2),$$

Oznake vodoravne pikčaste črte rešitev enačbe s sinusom, navpično - s kosinusom.

Tako lahko končno rešitev zapišemo na primer takole:

$$\left[ \begin(array)(l)x= \pm \frac(2\pi)(3),\\x = \frac(\pi)(3)+2\pi k. \end(niz)\desno.$$

Trigonometrična enačba z ODZ

$$(1+\cos x)\levo(\frac(1)(\sin x) - 1\desno) = 0.$$

Pomembna razlika v tem primeru je, da se v imenovalcu pojavi sinus. Čeprav smo podobne enačbe v prejšnjih lekcijah malo reševali, se je vredno podrobneje posvetiti ODZ.

ODZ

`\sin x \neq 0 \desna puščica x \neq \pi k`. Ko označimo rešitev na krogu, bomo to vrsto korenin označili s posebej preluknjanimi (odprtimi) točkami, da pokažemo, da `x` ne more sprejeti takih vrednosti.

rešitev

Zreducirajmo na skupni imenovalec, nato pa oba oklepaja izmenično enačimo na nič.

$$(1+\cos x)\levo(\frac(1-\sin x)(\sin x)\desno) = 0,$$

$$1+\cos x = 0 \text( ali ) \frac(1-\sin x)(\sin x) = 0,$$

$$\cos x = -1 \text( ali ) \sin x=1.$$

Upam, da reševanje teh enačb ne bo povzročalo težav.

Niz korenin - rešitev enačbe - je prikazan spodaj z rdečimi pikami. ODZ je na sliki označen z modro barvo.

Tako razumemo, da rešitev enačbe `\cos x = -1` ne zadovoljuje ODZ.
Odgovor bo samo niz korenov `x = \frac(\pi)(2) + 2\pi k`.

Reševanje kvadratne trigonometrične enačbe

Naslednja točka našega programa je reševanje kvadratne enačbe. V tem ni nič zapletenega. Glavna stvar je videti kvadratno enačbo in narediti zamenjavo, kot je prikazano spodaj.

$$3\sin^2 x + \sin x =2,$$

$$3\sin^2 x + \sin x -2=0.$$

Naj bo `t= \sin x`, potem dobimo:

$$3t^2 + t-2=0.$$

$$t_1 = \frac(2)(3), t_2 = -1.$$

Naredimo obratno zamenjavo.

$$\sin x = \frac(2)(3) \text( ali ) \sin x = -1.$$

$$\left[\begin(array)(l)x = \arcsin \frac(2)(3) + 2\pi k, \\ x = \pi - \arcsin \frac(2)(3) + 2 \pi k, \\ x = -\frac(\pi)(2) + 2\pi k. \end(niz) \desno.$$

Reševanje kvadratne enačbe s tangento

Rešimo naslednjo enačbo:

$$\novoukaz(\tg)(\mathop(\mathrm(tg)))(\tg)^2 2x - 6\tg 2x +5 =0, $$

Upoštevajte, da je argument tangente 2x in da boste dobili končni odgovor, ga boste morali deliti z 2. Naj bo torej `t=\tg 2x`

$$t^2 - 6t +5 =0, $$

$$t_1 = 5, t_2 = 1.$$

Povratna zamenjava.

$$\tg x = 5,\tg x = 1.$$

$$\left[\begin(array)(l)2x = \arctan(5)+\pi k, \\ 2x = \frac(\pi)(4) + \pi k. \end(niz) \desno.$$

Zdaj pa delimo oba niza z dva, da ugotovimo, čemu je dejansko enak `x`.

$$\levo[\begin(array)(l)x = \frac(1)(2)\arctan(5)+\frac(\pi k)(2), \\ 2x = \frac(\pi) (8) + \frac(\pi k)(2). \end(niz) \desno.$$

Tako smo dobili odgovor.

Zadnja enačba (zmnožek tangensa in sinusa)

$$\tg x \cdot \sin 2x = 0.$$

ODZ

Ker je tangens ulomek, katerega imenovalec je kosinus, potem v ODZ dobimo, da je `\cos x \neq 0 \Rightarrow x \neq \frac(\pi)(2)+\pi k.`

rešitev

$$\tg x =0 \text( ali ) \sin 2x = 0.$$

Te enačbe je enostavno rešiti. Dobimo:

$$x = \pi k \text( ali ) 2x = \pi k,$$

$$x = \pi k \text( ali ) x = \frac(\pi k)(2).$$

Zdaj pa najbolj zanimivo: ker smo imeli ODZ, moramo opraviti izbor korenin. Nastalo vrsto korenin označimo na krogu. (Kako to storite, je podrobno prikazano v priloženem videu.)

Z modro je označen ODZ, z rdečo so rešitve. Vidimo lahko, da bo odgovor `x = \pi k`.

S tem se konča peta lekcija. Ne pozabite vaditi reševanja enačb. Ena stvar je vedeti, kako napreduje rešitev na splošno, druga stvar pa je, da se osredotočite na rešitev določenega problema. Postopoma vadite vsak element reševanja problema. Zdaj je glavna stvar naučiti se kompetentno delati s trigonometričnim krogom, poiskati rešitve z njegovo pomočjo, videti ODZ in pravilno zamenjati kvadratne enačbe.

Naloge za usposabljanje

Reši enačbe:

• `2 \cos^2 \frac(x)(2) + \sqrt(3) \cos \frac(x)(2) = 0`,
• `3 (\tg)^2 2x + 2\tg 2x -1= 0`,
• `2\cos^2 3x - 5\cos 3x -3 =0`,
• `\sin^2 4x + \sin x - \cos^2x =0` (uporabi osnovno trigonometrično istovetnost),
• `4\sin^2 \levo(x-\frac(\pi)(3) \desno) - 3 =0`.

Dovolj je. Če imate kakršna koli vprašanja, kar vprašajte! Pusti všeček, če je bilo moje delo koristno :)

ODZ v logaritemskih enačbah.

Pozor!
Obstajajo dodatni
materiali v posebnem oddelku 555.
Za tiste, ki so zelo "ne zelo ..."
In za tiste, ki "zelo ...")

Na kateri točki smo se ujeli v past elementarnega primera? Ravno v trenutku izločanja logaritmov. Logaritmi so popolnoma izginili, skupaj z njimi pa so izginile tudi ustrezne omejitve pri odgovoru. Brez sledu. V matematiki se temu reče širitev ODZ.

Pa kaj zdaj, opustiti izločitev logaritmov!? Potem sploh ne bomo mogli ničesar rešiti ... Ne, ne bomo zavrnili. Šli bomo v drugo smer! V matematiki se ta problem rešuje na ta način.

Preden rešimo katerokoli logaritemsko enačbo, zapišemo ODZ. Po tem lahko z enačbo počnete, kar želite. Mislim, na vas je, da se odločite ...) Ko prejmete odgovor, morate le ugotoviti, ali so korenine vključene v ODZ. Vključene so popolne, pravilne rešitve. Tiste, ki niso vključeni, neusmiljeno vržemo ven. Te korenine so nastale med postopkom raztopine neodvisno; so odveč. Včasih se imenujejo takole: tuje korenine.

Kako snemati ODZ?

Zelo preprosto. Pazljivo preučimo izvirni primer. Ne rešujemo, ne transformiramo, natančno pregledati, in točno original! Je pomembno! In tudi enostavno je. V primeru iščemo nevarna mesta. to delitev na izraz z X, celo ekstrakcijo korenin iz izraza z x in logaritmi z X-ji.

Ne vemo, kaj je x, kajne? Primera še nismo rešili. Vendar smo trdno prepričani, da bodo tisti X, ki bodo dali deljenje z ničlo, pridobivanje kvadratnega korena iz negativnega števila in kršili omejitve glede logaritmov očitno niso primerni kot odgovor. Ti X-ji spremenijo originalni primer v nesmisel. Zato so takšne vrednosti x nesprejemljive. Vse druge vrednosti x bodo sestavljale ODZ. Razpon sprejemljivih vrednosti. To je vse.

V praksi je vse to veliko lažje narediti. Beremo in razumemo. Vzemimo isti primer:

log 3 (x 2 -3) = log 3 (2x)

Poglejmo primer in ugotovimo, da ni delitev, ni korenov, vendar enačba vsebuje izraze z X znotraj logaritma. Spomnimo se, da mora biti sublogaritemski izraz vedno večji od nič. Takole pišemo neposredno:

Opomba! mi nič se ni odločil! Enostavno smo zapisali obvezni pogoj Vse sublogaritemski izraz. Za vsi logaritem v primeru. Sistemski znak (zavit oklepaj) pomeni, da morajo biti ti pogoji izpolnjeni istočasno.

To je vse. ODZ posneto. Ni tako težko, kajne?

Kaj storiti z ODZ?

Torej, ODZ je bil zabeležen. Polovica dela je narejena). Kaj storiti s tem posnetkom? Tukaj imamo možnosti.

Prva možnost, univerzalna:

Rešimo sistem neenačb, ki smo ga zapisali za ODZ.

Rešujemo samo ODZ! Zaenkrat se ne dotikajmo samega primera! Dobimo vrednosti x, ki so sprejemljive za to enačbo. Kdor zna reševati sisteme neenačb, bo za naš DL prejel naslednji odgovor:

Tisti. Kot odgovor lahko uporabimo samo X-je, ki so večji od korena tri!

To je to, slame so se polagale. Zdaj lahko prevzamete sam primer. Prosto lahko odstranite logaritme in naredite vse druge transformacije - prvotne omejitve smo zapisali in jih shranili.

Po rešitvi same enačbe in prejetih odgovorih x 1 = 3; x 2 = -1, zlahka vidimo, da je kot odgovor primeren le x 1 = 3. Koren x 2 = -1 je manjši od korena tri, je tuj. Enostavno ga zavržemo. To je vse.

Dobro je za tiste, ki znajo reševati sisteme neenačb, kajne?)

In če z reševanjem sistemov neenačb, potem ... ne toliko? Kako biti?! Kako biti, kako biti ... Uči se! Če pa te res moti... Ok, samo zate! Metoda-svetloba.)

Druga možnost, samo za preproste enačbe.

Torej, ODZ smo zapisali v obliki sistema neenačb. Ta sistem morda ne bo rešen. Pustite, kot je, takole:

In zdaj, enega za drugim Te vrednosti nadomestimo v sistem neenakosti ODZ.

Za x 1 = 3:

Samo preštejemo in dobimo:

Vse je vredu. Obe neenakosti držita. To pomeni, da gre trojka skozi ODZ in gre naravnost nazaj.

Nadomestite drugi koren x 2 = -1:

Preštejemo in dobimo:

To je kategorično napačno! Minus dva ni več kot nič! To pomeni, da ta korenina ni vključena v ODZ. Preprosto se zavrže in ne povzroči nobenega odziva. Vse. Upoštevajte, da se koren vrže ven, če se vsaj ne prilega eno sistemska neenakost.

Tukaj je svetlobna metoda. Naj poudarim, da je ta metoda preprosta in očitna. Reševanje neenačb nadomesti preprosto računanje. Zelo dober v preprostih enačbah. In ni primeren za logaritemske neenakosti. Lahko uganeš zakaj?

Da, ker odgovor na neenakost običajno nima enega ali dveh korenov, ampak interval. Tisti. neskončno niz številk. In pri lahki metodi morate nadomestiti v ODZ Vse pomeni... Neskončnost. Kar se zdi malo težko, ja ...

Tukaj smo si ogledali le en preprost primer. A bistvo takšnega dela z DZ ostaja nespremenjeno za kaj logaritemske enačbe.

No, pa smo imeli opravka z ODZ - glavno pastjo v logaritemskih enačbah. Najbolj pozorni se lahko vprašajo, zakaj smo v prejšnji lekciji uspeli brez ODZ? Ja, samo ODZ ni v ničemer vplival na odgovor! Lahko preverite sami. Zgodi se. Odločili smo se, da se ODZ ne spomnimo (ali pa sploh ne vemo ...), a smo vseeno dobili pravilen odgovor. Tako srečen. Pravim, da je loterija, če se odločiš brez ODZ ...)

In zdaj - pozor!

Pojdi vanjo. In zapomni si eno preprosto misel. Ta misel vas bo rešila pred zmedo v vaši odločitvi in ​​zmedo v glavi:

Rešitev katere koli logaritemske enačbe je sestavljena iz dveh enakih delov. En del je reševanje same enačbe. Drugi je reševanje pogojev DL. Ti deli so rešeni ne glede na to drug od drugega. Rezultati se združijo v končni fazi rešitve.

Ključna beseda tukaj je "ne glede na". Pri reševanju ODZ se vam ni treba spomniti enačbe. In obratno. Glavna stvar je, da ne pozabite primerjati rezultatov na koncu, zavrzite presežek in zapišite pravilen odgovor.)

Povzemimo to v praktični nasvet.

Praktični nasveti:

1. Najprej zapišemo pogoje DL glede na izvirnik primer.

2. Izberemo, kje bomo začeli rešitev. Lahko začnete z enačbo ali pa s pogoji ODZ. Izberemo tisto, kar je lažje rešiti.

3. Po rešitvi enačbe in ODZ rezultate strnemo v splošen odgovor.

4. Če primer dovoljuje, DL ni treba rešiti. Dovolj je, da rezultate enačbe nadomestimo v zapisane pogoje ODZ in preverimo, katere rešitve so uspešne. Vzemite jih za odgovore.

No, kot ponavadi, bomo ugotovili. Tukaj je le nekaj primerov, ki pa zajemajo najbolj priljubljene žetone z ODZ. Nekateri triki (če jih vidite) vam omogočajo, da skrajšate rešitev desetkrat! Ne hecam se.

Poiščite koren ali vsoto korenin (če jih je več) enačb:

log 2 (x 2 +5x-6) = log 2 (4x)

ln(x 3 -7x+2sinx+3) = ln(x 3 -7x+2sinx-4)

Odgovori (v razsulu): 2; ni rešitev; 1; -5.

No, kako je? Opažam, da je strašljiv videz nekaterih primerov zavajajoč. Z lahkoto jih je mogoče rešiti.) Če ste vse naredili hitro in pravilno, se lahko lotite težjih nalog.

Če ni uspelo ali je reševanje trajalo dolgo, obiščite razdelek 555. Tam so ti primeri podrobno analizirani. Tehnike za pravilno in hitro rešitve. Včasih v logaritemskih enačbah polovice ali celo več sploh ni treba rešiti. Odgovor bo še vedno pravilen. Da Da! 555. člen to posebej poudarja.

Zdaj lahko povsem zanesljivo rešite preproste logaritemske enačbe. Ni loterija, ja ...)

In kako zmanjšati zapletene enačbe na najpreprostejše, kako v celoti uporabiti lastnosti logaritmov in zamenjave spremenljivk, kako ne pasti v zasedo, imenovano "Zoženje ODZ" - vse to bo v naslednjih lekcijah.

Če vam je všeč ta stran ...

Mimogrede, za vas imam še nekaj zanimivih spletnih mest.)

Lahko vadite reševanje primerov in ugotovite svojo raven. Testiranje s takojšnjim preverjanjem. Učimo se - z zanimanjem!)

Lahko se seznanite s funkcijami in izpeljankami.

Šamšurin A.V. 1

Gagarina N.A. 1

1 Občinska proračunska izobraževalna ustanova "Srednja šola št. 31"

Besedilo dela je objavljeno brez slik in formul.
Celotna različica dela je na voljo v zavihku "Delovne datoteke" v formatu PDF

Uvod

Začel sem z ogledom številnih matematičnih tem na internetu in izbral to temo, ker verjamem, da pomembnost iskanja DL igra veliko vlogo pri reševanju enačb in problemov. V svojem raziskovalnem delu sem preučila enačbe, v katerih je dovolj le najti ODZ, nevarnost, izbirnost, omejeno ODZ in nekatere prepovedi v matematiki. Zame je najpomembnejše, da dobro opravim enotni državni izpit iz matematike, za to pa moram vedeti: kdaj, zakaj in kako najti DL. To me je spodbudilo k raziskovanju teme, katere namen je bil pokazati, da bo obvladovanje te teme študentom pomagalo pri pravilnem opravljanju nalog na enotnem državnem izpitu. Za dosego tega cilja sem raziskoval dodatno literaturo in druge vire. Zanimalo me je, ali učenci naše šole vedo: kdaj, zakaj in kako najti ODZ. Zato sem opravil test na temo "Kdaj, zakaj in kako najti ODZ?" (Podanih je bilo 10 enačb). Število učencev - 28. so ga obvladali - 14%, nevarnost DD (upoštevano) - 68%, izbirnost (upoštevano) - 36%.

Tarča: identifikacija: kdaj, zakaj in kako najti ODZ.

Težava: enačbe in neenačbe, v katerih je treba najti ODZ, v tečaju algebre niso našle mesta za sistematičen prikaz, zato se verjetno z vrstniki pri reševanju takšnih primerov pogosto zmotimo, za reševanje porabimo veliko časa, ob tem pa pozabimo. glede ODZ.

Naloge:

1. Pokažite pomen ODZ pri reševanju enačb in neenačb.
2. Opravite praktično delo na to temo in povzamete njegove rezultate.

Mislim, da mi bodo pridobljena znanja in veščine pomagale rešiti vprašanje: ali je treba iskati DZ ali ne? Nehala bom delati napake tako, da se naučim pravilno izvajati ODZ. Ali mi to uspe, bo pokazal čas oziroma enotni državni izpit.

Poglavje 1

Kaj je ODZ?

ODZ je razpon sprejemljivih vrednosti, torej so to vse vrednosti spremenljivke, za katere je izraz smiseln.

Pomembno. Za iskanje ODZ ne rešujemo primera! Rešujemo dele primera za iskanje prepovedanih mest.

Nekaj ​​prepovedi pri matematiki. Takih prepovedanih dejanj je v matematiki zelo malo. A ne spomnijo se jih vsi ...

• Izrazi, ki so sestavljeni iz znaka sode množine ali morajo biti >0 ali enaki nič, ODZ:f(x)
• Izraz v imenovalcu ulomka ne more biti enak nič, ODZ:f(x)
• |f(x)|=g(x), ODZ: g(x) 0

Kako snemati ODZ? Zelo preprosto. Zraven primera vedno napišite ODZ. Pod temi znanimi črkami, če pogledamo izvirno enačbo, zapišemo vrednosti x, ki so dovoljene za izvirni primer. Preoblikovanje primera lahko spremeni OD in s tem odgovor.

Algoritem za iskanje ODZ:

1. Določite vrsto prepovedi.
2. Poiščite vrednosti, pri katerih izraz nima smisla.
3. Odstranite te vrednosti iz niza realnih števil R.

Reši enačbo: =

Razpon sprejemljivih vrednosti nas ščiti pred tako resnimi napakami. Iskreno povedano, prav zaradi ODZ se marsikateri “šok študent” spremeni v “C” študent. Ker menijo, da je iskanje in upoštevanje DL nepomemben korak pri odločitvi, ga preskočijo in se potem sprašujejo:»zakaj je učiteljica dala 2?« Ja, zato sem dal, ker je odgovor napačen! Ne gre za učiteljevo »gnido«, ampak za čisto specifično napako, tako kot napačen izračun ali izgubljen znak.

Dodatne enačbe:

a) = ; b) -42=14x+; c) =0; d) |x-5|=2x-2

2. poglavje

ODZ. Za kaj? Kdaj? kako

Razpon sprejemljivih vrednosti - obstaja rešitev

1. ODZ je prazna množica, kar pomeni, da izvirni primer nima rešitev

• = ODZ:

Odgovor: brez korenin.

• = ODZ:

Odgovor: brez korenin.

0, enačba nima korenin

Odgovor: brez korenin.

Dodatni primeri:

a) + =5; b) + =23x-18; c) =0.

1. ODZ vsebuje eno ali več števil, s preprosto zamenjavo pa hitro ugotovimo korene.

ODZ: x=2, x=3

Preverite: x=2, + , 0<1, верно

Preverite: x=3, + , 0<1, верно.

Odgovor: x=2, x=3.

• > ODZ: x=1,x=0

Preverite: x=0, > , 0>0, nepravilno

Preverite: x=1, > , 1>0, drži

Odgovor: x=1.

• + =x ODZ: x=3

Preverite: + =3, 0=3, napačno.

Odgovor: brez korenin.

Dodatni primeri:

a) = ; b) + =0; c) + =x -1

Nevarnost DD

Upoštevajte, da lahko transformacije identitete:

• ne vplivajo na DL;
• vodi do razširjenega DL;
• vodijo do zožitve ODZ.

Znano je tudi, da lahko zaradi nekaterih preoblikovanj, ki spremenijo prvotni ODZ, pride do nepravilnih odločitev.

Vsak primer ponazorimo s primerom.

1) Razmislite o izrazu x + 4x + 7x, ODZ spremenljivke x za to je množica R. Predstavimo podobne izraze. Posledično bo dobil obliko x 2 +11x. Očitno je tudi ODZ spremenljivke x tega izraza množica R. Izvedena transformacija torej ni spremenila ODZ.

2) Vzemite enačbo x+ - =0. V tem primeru je ODZ: x≠0. Tudi ta izraz vsebuje podobne člene, po redukciji katerih pridemo do izraza x, katerega ODZ je R. Kaj vidimo: kot rezultat transformacije se je ODZ razširil (število nič je bilo dodano ODZ izraza spremenljivka x za prvotni izraz).

3) Vzemimo izraz. ODZ spremenljivke x je določen z neenakostjo (x−5)·(x−2)≥0, ODZ: (−∞, 2]∪∪/Način dostopa: Materiali s strani www.fipi.ru, www.eg

Priloga 1

Praktično delo "ODZ: kdaj, zakaj in kako?"

Dodatek 2

Odgovori na naloge praktičnega dela "ODZ: kdaj, zakaj in kako?"